Antik óra Excelben

A múltkor felmerült a gondolat, hogy hogyan lehetne az Excel beépített diagramjait felhasználva napóra modellt készíteni. A dolog végül elment egy másik irányba, és napóra helyett antik óra lett belőle. A megoldás nem kifejezetten bonyolult, az eredmény ugyanakkor rendkívül látványos, és remekül szemlélteti, hogy Excelben olyan lehetőségek állnak rendelkezésre, amikre nem is gondolnánk elsőre.
Úgy gondoltam, érdemes közkinccsé tennem a Programozás rovatban, bár némi perverzióval besorolhatjuk a Szórakozás kategóriába is. :-)

A megoldás fő kérdései a következők:
- hogyan rajzolok antik mutatókat Excelben?
- hogyan forgatom el a mutatókat?
- mitől fog járni az óra?

A mutatók megrajzolása

A trükk az egészben az, hogy a mutató kontúrját, mint egy ponthalmazt írjuk le. Ízlés szerint kiválasztjuk a mutató jellemző pontjait, amiket összekötve megkapjuk a körvonalat. X és Y koordinátákkal megadott ponthalmazt pedig néhény kattintással megjeleníthetünk a Scatter diagramot használva. Azt a változatot választottam, amelyik nem töröttvonallal, hanem ívvel köti össze a pontokat. Ez jobban illik az antik dizájnhoz, más esetben jobb lehet az egyenes szakaszokkal körberajzolt mutató.
Lehetőleg úgy adjuk meg a koordinátákat, hogy a forgástengely a (0,0) pont legyen - ennek később az elforgatásnál lesz jelentősége, nem árt, ha a mutatók "értelmes" tengely körül járnak körbe.
Az eredményt az alábbi képen láthatjuk:

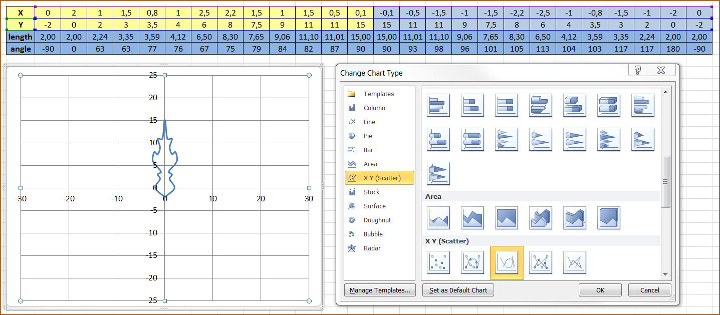
A mutatók forgatása

A mutatók minden pontja lényegében egy helyvektorral írható le, vektort meg aránylag könnyű forgatni, ha ismert a nagysága és az iránya. Ezért a mutató minden pontját át kell számítani polárkoordinátákra. A hosszt egyszerűen Pithagorasz-tétellel számíthatjuk. A szöget az X és Y koordináta arányából az arcus tangens függvénnyel tudjuk meghatározni, csak... a feladat nem teljesen triviális:
- mi van, ha az osztó nulla?
- X és Y hányadosának az előjelét az osztó és az osztandó együtt határozza meg, így kétféle X,Y pár esetén is ugyanazt a szöget kapjuk vissza. Ezért kicsit bonyolítani kell a képleten, konkrétan ha X van a C3 cellában, Y pedig a C4-ben, akkor
=IF(C3>0;ATAN(C4/C3)*rad2deg;IF(C3=0;IF(C4>0;1;-1)*90;ATAN(C4/C3)*rad2deg+180))
lesz a barátunk. :-) A képlet csak első ránézésre bonyolult, lényegében a következőt csinálja:
- ha X > 0, akkor alfa = arc tg (Y/X)
- ha X = 0, akkor alfa +90 fok vagy -90 fok az Y előjelétől függően
- ha X < 0, akkor alfa = arc tg (Y/X) + 180 fok
A következő kérdés az, hogy mennyivel kell az egyes mutatókat elforgatni. A mutatók a teljes 360 fokos kört különféle idő alatt teszik meg, így az egyes szögek:
- alfa(másodpercmutató) = sec/60 * 360 fok
- alfa(nagymutató) = (sec/(60*60) + min/60) * 360 fok
- alfa(kismutató) = (sec/(12*60*60) + min/(12*60) + óra/12) * 360 fok
Értelemszerűen a mutató minden pontját el kell forgatni ezzel a szöggel. A három mutatót egy diagramon megjelenítve lényegében kész az óra.
Arról nem szabad elfelejtkezni, hogy az Excel radiánban számol, a fenti képletben a rad2deg konstans a kettő között konvertál.

Mitől fog járni az óra?

Az óra járását az Excel VBA OnTime eseménye biztosítja, ami semmi mást nem csinál, csak másodpercenként aktualizálja a táblázatot, majd beállít egy újabb időzítést egy másodperccel későbbre. Mivel az időt a NOW() függvénnyel olvassuk ki, az óra minden másodpercben lépni fog.
Public Sub EventMacro()
Application.Calculate
alertTime = Now + TimeValue("00:00:01")
Application.OnTime alertTime, "EventMacro"
End Sub
Persze ehhez az is kell, hogy a fájl megnyitásakor elindítsuk az első időzítést:
Sub Workbook_Open()
alertTime = Now + TimeValue("00:00:01")
Application.OnTime alertTime, "EventMacro"
End Sub

És ezzel kész is vagyunk. A megoldás meglepően egyszerű, és első ránézésre szinte mindenki azt gondolja, hogy valami különösen bonyolult Visual Basic kód van mögötte. Mint a fentiekből láthatjuk, erről szó sincs – elég, ha ügyesen ki tudjuk használni az Excel beépített megoldásait.

Antik óra Excelben

A cikk utoljára frissítve: 2016.07.

Vissza a lap tetejére | Vissza a nyitóoldalra