|
|
Amikor eldőlt, hogy a középkonzol futurisztikus jelleget fog
ölteni, szinte azonnal adódott, hogy klasszikus, és kétségkívül mutatós ;-)
kivezérlésmérőt is le kellene cserélni valami modernebbre. A cél kizárólag a
látvány megváltoztatása volt, hiszen a mögötte levő hardver, és az adatok
beolvasása tökéletesen működik.
Nézegettem youtube-on, vannak gyönyörűséges hang vizualizációs megoldások, de
figyelembe kellett venni, hogy nekem mindezt Python-ban kellett megvalósítani,
egy Raspberry PI-n, ráadásul véges idő alatt.
| Mindenképpen valami geometrikus megoldásban gondolkodtam. Arra az
elképzelésre jutottam, hogy egy térben forgó test formáját fogom módosítani a
hangspektrum változásainak megfelelően. A választás végül a kis
csillagdodekaéderre esett. |
|
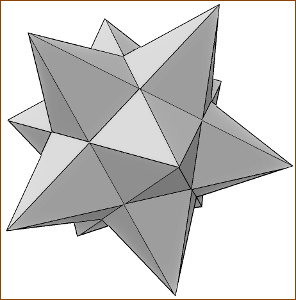 |
Ennek tizenkettes szimmetriája van, a spektrumanalizátor IC-ből ugyan
csak hét frekvenciasáv amplitúdója jön ki, de öt köztes frekvenciát simán ki
lehet számolni interpolációval, a lényeg úgyis a látvány, nem a halálpontos
mérés. Szóval úgy döntöttem, hogy a csillag ágainak hossza változik majd
szépen az amplitúdó függvényében. Értelemszerűen két test kell, egy a jobb és
egy a bal csatornának.
|
Persze, hogy ne legyen nagyon unalmas a látvány, még kitűztem magam
elé néhány célt a látványt illetően:
- legyen megvilágítva a test, jól beazonosítható irányból érkező fénnyel: a
fényforrás felőli oldalon legyen becsillanás, ha a test adott lapja éppen olyan
szögben áll, a másik oldalon viszont legyenek árnyékolva a lapok,
- a testek forogjanak a térben, véletlenszerűen változó forgástengely (!)
körül.
Na és ami innentől következik, az 100% töménységű koordinátageometria. Én
szóltam. :-) Azért gondoltam érdekesnek megírni a cikket, mert az eredmény jól
mutatja, hogy egyszerű, de mégis látványos 3D grafikát középiskolai szintű
matekkal is lehet csinálni, mindenféle csilivili 3D motor nélkül is. És persze
ha valaki bele akar mászni a 3D grafika rejtelmeibe, akkor amúgy sem árt, ha
tisztában van néhány dologgal. Lássuk.
Néhány koordinátageometriai alapfogalom
... amikre mindenképpen szükség lesz, feltételezve, hogy azon már
túl vagyunk, hogy egy térbeli pontot három koordinátával lehet azonosítani,
meg hogy mi az a vektor. Ha ezek nincsenek meg, akkor ne akarj 3D grafikával
foglalkozni.
| Normálvektor
: a normálvektor egy adott síkra merőleges, egységnyi
hosszúságú vektor. Ilyenből kettő van, ha a sík vízszintes, akkor az egyik
felfelé néz, a másik lefelé, tehát pontosan ellentétes irányúak. Fontos, hogy
melyik melyik. Zárt testről lévén szó, azt célszerű használni, amelyik a
testből kifelé mutat. A normálvektor a síknak nagyon fontos jellemzője, az
összes műveletben, mint láthatóság, fénycsillanás, árnyékolás számítása,
megjelenik. Noha a normálvektor alapvetően egy sík jellemzője, a fogalmat én
síkidomokra (jelen esetben háromszögekre) vonatkoztatva fogom használni, a
kettő egyenértékű. |
 |
Skaláris szorzat
: A skaláris szorzat egy szám, lényegében
azt mutatja meg, hogy mennyire "egyirányú" két vektor. Két egységvektor
skaláris szorzata 1, ha egy irányba mutatnak és párhuzamosak, 0 és 1 között
van, ha hegyesszöget zárnak be, 0 akkor, ha merőlegesek, -1 és 0 között van,
ha tompaszöget zárnak be, és -1 akkor, ha párhuzamosak, de ellentétes
irányúak. A skaláris szorzat a láthatóság és a fénycsillanások ill.
árnyékolások számításakor lesz majd hasznos.
Vektoriális szorzat
: A vektoriális szorzat egy vektor, aminek a
legfontosabb jellemzője, hogy merőleges a szorzatot alkotó két vektorra.
Alapvetően a normálvektor kiszámítására fogjuk használni. Egy ABC háromszög
normálvektora az ABxAC szorzat,
egységnyi hosszra normálva.
Az egyszerűség kedvéért a szorzatok számításakor mindig egységnyi hosszúságú
vektorokat használunk.
Leképezés
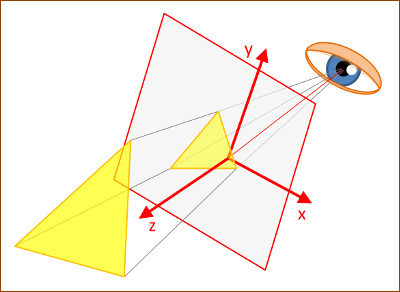 |
A 3D grafika első kérdése természetesen az, hogy hogyan lesz egy térbeli
tárgyból síkbeli kép. Ez a folyamat a leképezés. A tárgyat egy adott
nézőpontból nézzük, a fény az egyes pontokról egyenes vonalban jut a
szemünkbe, illetve 3D grafika esetében a nézőpontba. A kettő között
helyezkedik el a képsík, és ahol a tárgy adott pontjából a nézőpontba tartó
egyenes átlépi a képsíkot, ott lesz az adott pont képe. A számítások általános
helyzetű nézőpont és képsík esetében meglehetősen bonyolultak, a bonyolult
számítás pedig a sebesség halála, ezért az egyszerűség kedvéért a nézőpontot a
z tengelyre "szokás" tenni (vagyis az x és y koordinátái nullák), a képsík
pedig a z=0 sík (tehát az a sík, ami az x és y koordinátatengelyeket
tartalmazza). |
Ennek a transzformációnak a legfontosabb jellemzője, hogy az
egyenesek egyenesek maradnak. Vagyis ha egy háromszöget képezünk le, akkor
annak a képe is egy (valószínűleg más formájú) háromszög lesz. Így elég, ha
kiszámítjuk a három csúcs képét, és azokat összekötve megkapjuk a háromszög
képét. (Textúrákkal most nem foglalkozunk.) A háromszög egyébként ténylegesen
a 3D grafika leggyakoribb építőeleme. A leképezés egyenletei - az előzőekben
írt feltevésekkel - meglehetősen egyszerűek:
def projecttoplane(self, viewz):
# By default, viewpoint is on the z
axis
 zratio = -viewz / (self.z - viewz)
# Ratio of
projection
zratio = -viewz / (self.z - viewz)
# Ratio of
projection
 self.px = math.trunc(zratio * self.x)
# Calculate screen position
self.px = math.trunc(zratio * self.x)
# Calculate screen position
 self.py = math.trunc(zratio * self.y *
const.VSCALE)
# y axis points down if viewz < 0
self.py = math.trunc(zratio * self.y *
const.VSCALE)
# y axis points down if viewz < 0
Nem látható lapok kezelése
A második legfontosabb kérdés az, hogy honnan tudjuk, mely lapokat
kell kirajzolni, és melyeket nem. A lapok takarhatják egymást részlegesen és
egészen. Ha a megjeleníteni kívánt test zárt (vagyis nincs olyan lapja, aminek
mind a két oldala a külvilág felé nézne), akkor van egy nagyon egyszerű
szabály: azok a lapok, amik nem a nézőpont felé néznek, nem látszanak, mert
biztosan vannak előttük más lapok, amik takarják őket.
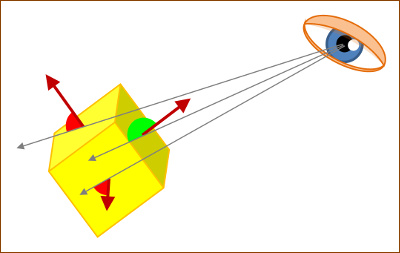
| Ezzel rajzoláskor gyakorlatilag azonnal kiszórhatjuk a lapok nagyjából
felét, persze kell tudni, melyik felét. :-) Azok a lapok
nem
fognak
látszani, amelyeknek a normálvektora a nézőpontból az adott lap bármely
pontjába irányuló vektorral hegyesszöget zár be (az ábrán pirossal jelölt
szögek). Ezt pedig, a fent leírt módon, a skaláris szorzat előjele alapján
lehet eldönteni. A számításhoz a háromszög súlypontját, mint középpontot
használom. |
 |
Egymást részlegesen takaró lapok kezelése
Ezt a problémát – mivel a megjeleníteni kívánt test relatív
egyszerű - úgy kezeljük, hogy távolság szerint csökkenő sorrendben rajzoljuk
ki a háromszögeket. Mivel semelyik két háromszög nem metsz bele egymásba,
amelyiknek a középpontja távolabb van, azt kell hamarabb kirajzolni és
kész.
Vagyis a kirajzoláskor először végignézzük, melyek azok a háromszögek, amik a
nézőpont felé néznek, majd ezeket távolság szerint csökkenő sorrendben
megrajzoljuk.
Csillanások és árnyékok számítása
Csak a pontosítás kedvéért: nem vetített árnyékról van szó, hanem
arról, hogy a test lapjai mennyit veszítenek a világosságukból amiatt, hogy a
megvilágítás közvetlenül nem éri őket.
A becsillanás és az árnyék két külön számítás eredménye (lásd megjegyzés, a
modellben csak egyet használok). Becsillanás akkor következik be, amikor a
fényforrásból érkező fény a nézőpont irányába tükröződik vissza. Egy ideálisan
tükröző felület esetén ez pontosan egy adott szögben álló lap esetében áll
elő, viszont minél diffúzabb a felület, annál szélesebb tartományban. A másik
véglet a tökéletesen diffúz felület (mint egy ideális mozivászon), ami a beeső
fényt minden lehetséges irányba szórja. Mivel a bejövő fényenergia konstans,
annál világosabbnak látjuk a becsillanást, minél szűkebb tartományra
korlátozódik.
Tükröződéskor a beeső és a visszavert fénysugár egyenlő szöget zár be a
felület normálvektorával, ráadásul egy síkba esnek, így a normálvektor
lényegében felezi a beeső és a visszavert fénysugarak alkotta
szöget.
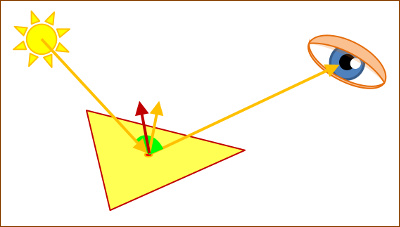 |
Ahhoz, hogy megállapítsuk, a visszavert fény mennyire jut a szemünkbe,
illetve a nézőpontba, a következő számítást használjuk:
- megkeressük az adott lap középpontját,
- kiszámítjuk a fényforrásból jövő fény és a lap középpontjából a nézőpontba
futó fénysugár alkotta (az ábrán zöld) szög szögfelezőjét (az ábrán a kis
narancssárga vektor),
- megnézzük, hogy az így kapott vektor mennyire párhuzamos a felület
normálvektorával (az ábrán a barna vektor), vagyis kiszámítjuk a két vektor
skaláris szorzatát. Minél közelebb van a skaláris szorzat 1-hez, annál
közelebb vagyunk a tükröződéshez, vagyis annál erősebb a becsillanás. |
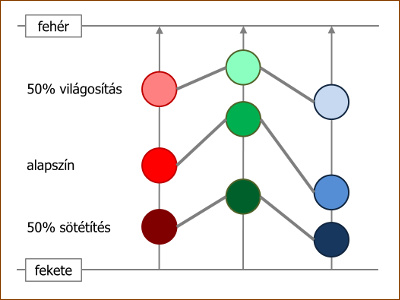
| A lap színének megvilágítástól függő változását úgy modellezzük, hogy a
lap alapszínét vagy elhúzzuk fehér felé, vagy eltoljuk a fekete felé a
skaláris szorzat előjelétől függően. Érdemes megjegyezni, hogy a két művelet
eltérő számítást igényel. Sötétítés esetén simán megszorozzuk az R, G, B
értékeket egy egynél kisebb számmal, míg világosításnál az adott R, G, B
értékek
fehértől való különbségét
csökkentjük arányosan, nem csak simán
megszorozzuk őket. |
 |
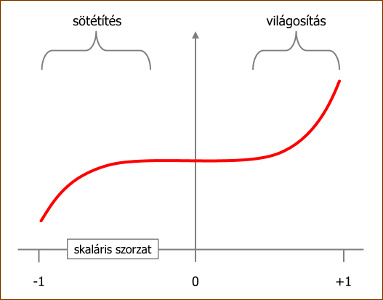 |
A felület simaságát egy általunk választott, a sötétítést és
világosítást leíró függvénnyel tudjuk modellezni. Ennek a görbéje valami
hasonló lesz, mint az ábrán. Érdemes megfigyelni, hogy a sötétítés nem
nulláról indul. Ha onnan indulna, akkor a fényforrástól elfelé néző lapok
feketék lennének.
A jobb oldali szakasz meredeksége és legnagyobb értéke határozza meg a
becsillanás intenzitását. Meredek felfutás és teljesen fehér színig húzás
esetén vakító becsillanást fogunk kapni, mint egy nagyon sima és tükröződő
felület esetén. Értelemszerűen, minél meredekebb a függvény felfutása, annál
ritkábban kapunk majd becsillanást a véletlenszerű forgás miatt, hiszen annál
ritkábban kerül egy lap pont olyan szögbe. |
Megjegyzés: az árnyék/sötétítés számítása ebben a formában
fizikailag abszolút nem korrekt. A hétköznapokban a test egy nem tökéletesen
fényelnyelő környezetben van (ha abban lenne, a közvetlen fényt nem kapó
részei nem látszanának, lásd félhold), hanem a környezet visszaveri
a fényt a tárgyak árnyékos oldalára, ezért látszanak egyáltalán. Ennek a
pontos modellezése rendkívül bonyolult számításokat igényelne. A leírtak
tehát egy nagyon erősen leegyszerűsített képét adják a valóságnak. A dolog
szépsége, hogy az eredményül kapott látvány így is hihető.
Fizikai modell
A fizikai modellnél semmi újat nem akartam kitalálni, a csúcsok
mozgása lényegében megegyezik az első verzió mutatós műszer szimulációjával
(lásd a Hivatkozott oldalak részben).
Optimalizálás
Az elkészült kód első verzióban nagyjából kőkemény 21.1 fps-sel
futott :-), ez azért nem egy szemkápráztató teljesítmény. Próbáltam megnézni,
hogyan lehetne gyorsítani. A legegyszerűbb megoldás nyilván a képernyőfelbontás
csökkentése lett volna, de ezt úgy éreztem, megfutamodás lenne a kihívások
elől :-), úgyhogy máshol keresgéltem tovább. A kód optimalizálás mindig nagyon
tanulságos tud lenni.
Ahhoz, hogy optimalizálni tudjunk, érdemes elemezni, hogy mi mennyi időt vesz
igénybe a futásban. Első körben a 21.6 fps 49.3 ms képfrissítési időnek felel
meg. Néhány méréssel megállapítható, hogy a következő részek
kikerülhetetlenek:
- tengelyek forgatása, soros kommunikáció, képfrissítés, stb: 7.5 ms,
- dodekaéderek kirajzolása: 6.6 ms.
Az alapváltozatban tehát egy dodekaéder kiszámítása 14.3 ms időbe telt.
Első menetben lecseréltem a fény-/árnyékhatást számoló függvényt adattábla
olvasásra. Memória van rogyásig, így létrehoztam egy kétdimenziós tömböt,
egyik dimenzió a szín 0-tól 255-ig, a másik pedig a skaláris szorzat 0.01
pontossággal. Ez ugye egy kb. 50 ezer adatot tartalmazó táblázat, szóval nem
kicsi, viszont csak egyszer kell feltölteni, a táblázatban keresés pedig gyors.
Eredmény: a képernyőfrissítés felmászott 21.8 fps-re, ami abszolút értékben
nem sok, de százalékosan igen: az idő 3%-át meg lehetett spórolni ezzel az
egy módosítással.
Következő körben kiszórtam a redundáns számításokat, minden adatot, amivel
egynél többször kell számolni, külön változóba tettem. Meglepő módon érdemben
nem gyorsult a futás.
A további gyorsításhoz mélyebb módosításra volt szükség. A program első
változatában a lapokat alkotó háromszögek csúcspontjai redundánsan voltak
jelen, és a minden egyes pont leképezése a képernyőre háromszor megtörtént.
A háromszög egy "önálló életet élő" objektumként szerepelt a kódban. Ezt
átalakítottam olyan formában, hogy a csúcspontok kapták meg azokat a
számításokat, amik a leképezéshez kellenek, és a háromszögek már csak a
csúcspontok listájában keresgélnek. (Természetesen vannak funkcionalitások,
amiknek muszáj a háromszögnél maradni, mint pl. normálvektor számítása.)
Ezzel nem csak számításokat, hanem rengeteg értékadó műveletet is
sikerült megtakarítani, és még a kód is olvashatóbb lett. Ráadásul az így
kivett redundancia elég jelentősnek bizonyult: a sebesség felugrott 26.4
fps-re, ami újabb 21%-os gyorsulás.
Már csak egy dolog maradt hátra: a forgatási mátrixot továbbra is minden egyes
csúcsponthoz külön számolta ki a program. Ez megint erősen redundáns, nagyon
számításigényes, és egy dodekaéderhez elég egyszer megcsinálni. Ezt
megváltoztatva a képfrissítés 29.4 fps-re ugrott. Ez azt jelenti, hogy egy
dodekaéder kiszámításához már csak 6.6 ms időre van szükség, ami az eredeti
időigény 46%-a, vagyis kevesebb, mint fele.
| Ezen a ponton elengedtem a kérdést. :-) Az eredményről raktam fel egy kis
videót youtube-ra. |
|
Végszó
| Természetesen vannak még érdekességek jócskán a programkódban :-),
de ami a 3D grafika részét illeti, ez az a témakör, amit szerettem volna
részletesen leírni. Akit érdekelnek a kihívások, nézze meg a kódban a
véletlenszerűen változó forgástengely körüli forgás megvalósítását - ezt
kifejezetten nehéz volt úgy megoldani, hogy ne legyen darabos a testek
mozgása. A forráskód megtalálható a Letöltések rovatban, a pygame könyvtár
kell a futtatásához. A Linkek rovatban pedig egy youtube videót találtok,
ami a működést mutatja. |
|
Aztán végül úgy döntöttem, hogy mégsem ezt a megjelenítést fogom
használni, mert vizuálisan nem simul bele kellően az új dizájnba, ahogy
eredetileg gondoltam. :-)
Új változat
Szóval a dodekaéderes verzió nagyon szépen ment, de úgy éreztem,
mégsem ezt akarom. Úgy gondoltam, talán jobb lenne, ha a műszerfal dizájnja
megjelenne a kivezérlésmérőben is. Vagyis (szimulált) LED gyűrűk, és persze
kellően látványos skálák.
A koncepció végül az lett, hogy az eredeti VU mérők helyett két, egymásba
fonódó gyűrű szimbolizálja az erősítőket, kétszer kettő plusz egy gyűrű pedig
a hangszórókat. A spektrumanalizátor IC-ről hét sáv jön le, ebből csinálok
hatot (a felső kettőt összevonva, azokat a frekvenciákat már úgyse nagyon
hallom :-)), a hatból egy lesz a szub, három a mélyközép, kettő a magas. Ez
persze nem teljesen korrekt, de megjelenítésnek kellően hatásos. Az erősítőből
a hangszórók felé menő jelet pedig külön megjelenítem futó fénypontokkal, mint
ahogy a mai hibrid autók mutatják az energiaáramlást a rendszerben. Plusz lesz
bekapcsolási küszöbszint külön az erősítő és külön a hangszóró
szimbólumokon.
Ez így elég bonyolultan hangozhat :-), de a megvalósítása programból sima
ujjgyakorlat. Ami viszont kellően sok munkát igényel, az a kivezérlés egyes
fázisainak megrajzolása. Mivel a kivezérlésmérő szabálytalan alakú, sokkal
hatékonyabb az előre elkészített képekből összerakni a megjelenítendőt, mint
menet közben matekozni. Így viszont 180 képet kellett egyesével megrajzolni és
elmenteni. Ezzel azért elvoltam egy darabig...
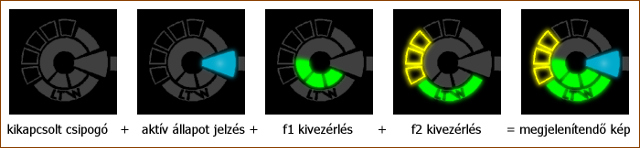
| A fenti kép szemlélteti, hogyan áll elő a kivezérlés az egyes
elemekből. A megoldás azért működik így, mert a grafikához használt pygame
könyvtárnak van egy olyan funkciója, hogy az egyik kép másikra másolását
BLEND_MAX
módban végezze, ilyenkor a két kép egymásra kerülő pixelei
közül a világosabbak jutnak érvényre. Mivel a világító LED-ek képe mindenhol
nagyobb RGB értékeket tartalmaz, mint a kikapcsolt, és csak ezek másolódnak rá
a képre, az egyes képelemek szépen összefésülhetők. A képfrissítés... nos, az
határeset, a 3-mas Raspberry éppen, hogy tud megfelelő sebességet. |
|
A cikk utoljára frissítve: 2018.01.
Kivezérlésmérő (2015.06.)
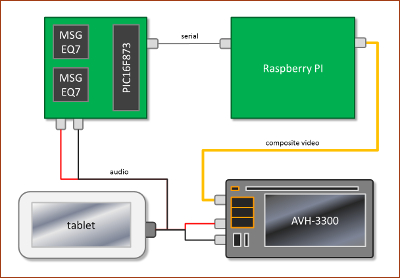
Nagyon rég volt már programozásos téma, de most az "Internetet az
autóba!" projekt kapcsán volt egy jó kis fejlesztés, amire érdemes pár szót
...
 Tovább a cikkhez Tovább a cikkhez
|
|
| |
|
|
Vissza a lap tetejére |
Vissza a nyitóoldalra
|
