|
|
| Gondolom, már ismerős az eljárás, ami a textúra leképezést végzi
(ami engem illet, én a GameDev.Net oldalon találtam meg, az oldal egyébként
elég jó), és érdekelne, hogy működik az egész, minek ide a vektorszorzás, meg
ilyesmi. Érdekes módon nem találtam meg a neten az algoritmus leírását, így
nekiálltam magamtól a visszafejtésnek. |
|
Nos, feltéve, hogy a vektorok fogalma ismerős, íme a magyarázat.
Egyszerűen addig alakítgatom az egyenleteket, amíg azt nem kapom, amit az
eljárás használ.
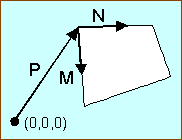 |
Nos, kezdjük! A definíciók szerint P a poligon egyik
tetszőleges sarka, M és N pedig két
lineárisan független (de nem feltétlenül merőleges) vektor a poligon síkjában.
Lásd a rajzot a bal oldalon.
Az algoritmus feltételezi, hogy |M| és
|N| a poligon oldalainak méretei. Ebben az esetben a
textúra éppen 1x1-szer fér el a poligonon. Ha a vektorok méretét felére
csökkentjük, 2x2 textúrát kapunk a poligonon stb. |
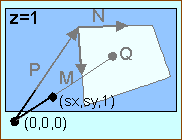
A poligon egy tetszőleges pontja (vagy ekvivalensen a pont helyvektora) -
legyen ez Q - leírható a P,
M és N vektorok kombinációjaként.
Q=P+u*M+v*N
Vetítsük Q-t a képernyőre! A nézőpont legyen az origóban
van, a vetítési sík z=1. Így a pont vetítőegyenletei meglehetősen egyszerűek
lesznek.
Qy/sy=Qz/1, és így Qy=sy*Qz.
Hasonlóan, Qx=sx*Qz. |
 |
Visszaírva ezeket Q egyenletébe, ezt kapjuk:
Qz*{sx,sy,1}=P+u*M+v*N
Ez kifejtve három egyenletet jelent Qz-re, u-ra és v-re, amit a rögös úton
járva elvileg ki lehet számítani. Szerencsére tudjuk, hová szeretnénk eljutni,
így egy kicsit könnyebb a dolog. :-)))
Számítsunk skalárszorzatot, a fentieket megszorozva
(PxN)-nel:
Qz*S.(PxN)=
P.(PxN)+
u*M.(PxN)+
v*N.(PxN)
Itt jön a lényeg: minden a és b
vektorra, a.(axb)
nulla, hiszen a két vektor vektoriális szorzata merőleges a vektorokra, viszont
két merőleges vektor skaláris szorzata nulla. Ettől sokat egyszerűsödik az
egyenlet:
Qz*S.(PxN)=
u*M.(PxN)
Persze meg kell szabadulnunk Qz-től. Ehhez szorozzuk meg az eredeti egyenletet
mégegyszer, ezúttal (NxM)-mel:
Qz*S.(NxM)=
P.(NxM)+
u*M.(NxM)+
v*N.(NxM), és
így
Qz*S.(NxM)=
P.(NxM)
Már látszik a vége! :-) Osszuk el a kettőt:
(S.(PxN))/
(S.(NxM))=
u*(M.(PxN))/
(P.(NxM))
Szerencsére, tud(hat)juk, hogy
(axb).c=
(bxc).a=
(cxa).b, és így
(S.(PxN))/
(S.(NxM))=u, és ez
pontosan az, amit ki akartunk számítani. v hasonlóan kapható meg:
(S.(MxP))/
(S.(NxM))=v
(Vektoriális szorzáskor figyelni kell a vektorok sorrendjére!)
Most már csak végig kell futtatni sx-et és sy-t a poligonon, és a
fenti képlet megadja a textúra koordinátákat. És ennyi az egész.
Még egy dolog érdekes lehet: amennyiben valaki "depth fogging"-ot
akar számolni, szüksége lesz Qz értékére. Ez a fentiek alapján könnyen
számítható, például:
Qz=(P.(NxM))/
(S.(NxM))
A cikk utoljára frissítve: 2006.01.
Vissza a lap tetejére |
Vissza a nyitóoldalra
|