Megoldások a fejtörőkhöz

Körmére ég a... kanóc

Az egyik kanócot meggyújtjuk mindkét végén, a másikat az csak egyik végén. A mindkét végén égő kanóc pontosan félóra alatt ég le (és ez független attól, hogy az égés egyenletes-e vagy sem!). Ezután meggyújtjuk a másik kanóc másik végét is, és az abból megmaradt "félórányi" darab negyedóra alatt ég le.

Kapcsoltam

Fekapcsolunk két kapcsolót, majd néhány perc múlva az egyiket lekapcsoljuk és átmegyünk a másik szobába. Az a lámpa, amelyik ég, a felkapcsolt kapcsolóhoz tartozik. A két lekapcsolt lámpa közül az egyik meleg lesz, az amelyiknek a kapcsolója fel volt kapcsolva.

Kapcsoltam II - a börtönben

Tegyük fel, hogy a kapcsoló A állásban van.
A rabot kijelölnek maguk közül valakit, ő lesz majd a legvégén, aki a bejelentést teszi. Őt nevezzük a továbbiakbak "Számlálónak".
Ezek után a kapcsolási szabályok:
1. Ha NEM a Számláló megy sétálni: ha az illető először sétál, és a kapcsoló A állásban van, akkor átkapcsolja B állásba, különben nem kapcsol. Ezáltal a Számlálón kívül minden rab egyszer fog kapcsolni.
2. Ha a Számláló megy sétálni, és a kapcsoló A állásban van, nem csinál semmit. Ha a kapcsoló B állásban van, akkor visszakapcsolja A-ba, és regisztrálja, hogy megint volt valaki sétálni. Ha elért n-1-ig a számolásban, akkor kijelentheti, hogy már mindenki volt sétálni.
Már csak az a dolgunk, hogy kiküszöböljük azt a tényt, hogy a kapcsoló kezdeti állása nem ismert, így a Számláló nem tudhatja, hogy ha az ő első sétájakor a kapcsoló B állásban van, akkor azért van B-ben, mert valaki A-ban találta és átkapcsolta, vagy azért, mert eleve B állásban volt. Ezért mindenkinek kétszer kell kapcsolnia, az első és a második esetben, amikor séta közben a kapcsolót A állásban találja. Ugyanis ebben az esetben, ha a Számláló 2*(n-1) kapcsolást regisztrált, két eset lehetséges:
a. A kapcsoló kezdetben A állásban volt, az összes többi rab kapcsolt már kétszer.
b. A kapcsoló kezdetben A állásban volt, volt n-2 rab, akik már kétszer kapcsoltak, és egy rab, aki egyszer (de ugye ezért biztos, hogy már ő is volt legalább egyszer sétálni).
Tehát 2*(n-1) kapcsolás után már mindenki volt biztosan legalább egyszer sétálni.

Oroszlánok a szigeten

Ha egy oroszlán lenne, így gondolkodna: ha megeszem a húst, engem senki nem tud megenni, így nem eshet bajom.
Ha ketten vannak, akkor így gondolkodik: ha megeszem a húst, a másik oroszlán meg fog enni engem az előző gondolatmenet miatt.
Ha három oroszlán van, azt mondja az első: ha megeszem a húst, két oroszlán marad ébren. A kettőből egyik sem fog engem megenni az előző gondolatmenet miatt. Így megehetem a húst.
Ha négy oroszlán van, akkor azt mondja az első: ha megeszem a húst, három oroszlán marad ébren. A háromból az, amelyik megtalál, meg fog engem enni az előző gondolatmenet miatt. Így nem ehetem meg a húst.
Továbbragozva a dolgot, ha "2n" oroszlán van, az, amelyik megtalálja a húst, nem eheti meg. Ha "2n+1" oroszlán van, akkor igen. Így 25 oroszlán esetén az első meg fogja enni a húst.

Lyukas csónak

Amíg a csónakon nincsen lyuk, a felhajtóerő szempontjából a csónak és a benne levő víz egy testnek minősül, aminek az átlagos sűrűsége nagyobb a fa sűrűségénél, de kisebb a víz sűrűségénél. A pontos érték a csónak arányaitól függ, de vélhetően elég közel lesz az 1-hez (a csónak fala elég vékony a térfogatához képest). Ezért a csónak alig fog kiemelkedni a vízből.
Ha lyukat fúrunk a csónak fenekébe, akkor a csónakon belül és kívül kiegyenlítődhet a szintkülönbség. Ebben az esetben a felhajtóerőt csak a csónak súlya határozza meg, a kiemelkedés mértékét pedig a csónak anyagának sűrűsége. Ha a fa sűrűsége 0.6 körüli, akkor a csónak annyira felemelkedik, hogy akár a víz harmada is kifolyhat belőle.

Szélcsend

A Föld forgása miatt a hajó egy tömegpontnak tekinthető, ami forog a Föld tengelye körül, és így van impulzusmomentuma, ami a tehetetlenségi nyomatékkal és a szögsebességgel egyenesen arányos. Ha felhúzzák a horgonyt, feljebb kerül a tömegközéppont, ezáltal megnő a sugár, és így a tehetetlenségi nyomaték. Az impulzusnyomaték-megmaradás miatt lecsökken a szögsebesség, a hajó lemarad a Földhöz képest. Mivel a Föld nyugatról keletre forog, a hajó nyugatra fog elindulni (persze nem sokáig, csak amíg a közegellenállás le nem fékezi).

Végtelen nagy ellenállás ;-)

Válasszunk ki egy rácspontot, és pumpáljunk bele I áramot. Mivel a rács végtelen, ezt gond nélkül megtehetjük. A rács szimmetriája miatt mind a négy irányba I/4 áram fog elfolyni.
Az előző esettől függetlenül, válasszunk ki egy rácspontot, és szívjunk ki ezen a ponton I áramot. Mivel a rács végtelen, ezt is gond nélkül megtehetjük. Itt mind a négy becsatlakozó irányból a szimmetria miatt I/4 áram fog befolyni.
A szuperpozíció elve alapján a dolog akkor is működik, ha ezt a két dolgot egyszerre csináljuk. A két kiválasztott csomópont legyen a rács egy élének két végpontja. Ekkor ezen az élen 2*I/4=I/2 áram fog folyni, vagyis a másik I/2 áram folyik a rács összes többi elemén. Így a végtelen rács eredője megfelel két párhuzamosan kapcsolt R ellenállásénak, vagyis R/2.

Megcsalt férjek

Biztos, hogy van a faluban legalább egy hűtlen feleség. Ha én nem tudok egy hűtlenről sem, akkor az én feleségem hűtlen és hétfőn délben ott lesz a templom lépcsőjén a holttest.
Ha én egy hűtlenről tudok, akkor még nem biztos, hogy tényleg csak egy van. Ha azonban hétfőn délben nincsen holttest, akkor mindenki tudott legalább egyről, azaz minimum két hűtlen van. Mivel én pontosan egyről tudok ezért az én feleségem a másik hűtlen és kedden délben ott lesz a templom lépcsőjén a két holttest.
Ha én két hűtlenről tudok, akkor kedden sem ölhetem még meg, mivel lehet, hogy tényleg csak két hűtlen van. Ha azonban kedden délben sincsen holttest, akkor mindenki tudott legalább kettő hűtlenről, azaz minimum három hűtlen feleség van. Mivel én pontosan kettőről tudok, ezért az én feleségem a harmadik hűtlen és szerdán délben ott lesznek a templom lépcsőjén a holttestek.
Ha én három hűtlenről tudok, akkor szerdán sem ölhetem még meg, mivel lehet, hogy tényleg csak három hűtlen van. Ha azonban szerdán délben sincsen holttest, akkor mindenki tudott legalább háromról, azaz minimum négy hűtlen van. Mivel én pontosan háromról tudok, ezért az én feleségem hűtlen és csütörtök délben ott lesz a templom lépcsőjén a négy holttest.
Ezzel el is értünk a megoldáshoz. A négy holttest csütörtökre kerül a templom lépcsőjére, mivel minden ember ugyanígy gondolkodik a faluban.
A gondolatmenetet akármeddig lehetne folytatni, tehát péntek délben már öt holttestnek kellene lenni, stb.

A madzag súlya

Hát ez bizony számolásos feladat... :-)
Miután elvágtuk a (jobb oldali) felfüggesztést, a madzag három részre osztható:
- A bal oldali rész, ami nem mozog, és így csak a súlyával terheli a felfüggesztést.
- A jobb oldali rész, ami szabadon esik.
- A kettő közötti dl hosszúságú szakasz, amit a szabadesés után meg kell állítani.
Az aránylag nyilvánvaló, hogy a legnagyobb erőt az utolsó dl hosszúságú darabka lefékezésekor fogjuk kapni, hiszen egyrészt ekkor már l-dl hosszúságú madzag lóg, másrészt ezt a darabkát kell a legnagyobb sebességről lefékezni. Konkrétan:
l-dl=g/2*t², hiszen a darabka l-dl hosszan esik szabadon. Mivel dl<<l,
SQR(2*l/g)=t ideig tart a zuhanás. Ekkor a sebesség
v=g*t=SQR(2*l*g).
Ezt a darabkát kell lefékezni dl úton, dt idő alatt, vagyis (egyenletes lassulást feltételezve)
dl=a/2*dt² és emellett
v=a*dt. Kiküszöböljük dt-t, mert minket a fékezéshez szükséges erő érdekel:
dt=v/a,
dl=a/2*(v/a)²=v²/(2*a)=2*l*g/(2*a),
dl=l*g/a,
a*dl=l*g. Mivel a madzag tömege m, és Newton II. törvénye szerint F=m*a, be kell hoznunk a tömeget. Jelöljük az egységnyi hosszúságú madzag tömegét M-mel, ekkor nyilván
m=M*l, illetve
dm=M*dl. Ebből
a*dm/M=m/M*g, vagyis
a*dm=m*g. A bal oldal a dm tömegű darabka fékezéséhez szükséges erő, és ez éppen a madzag súlyával egyezik meg, tehát az utolsó pillanatban a felfüggesztési pontot a madzag súlyának kétszerese terheli.

Homokóra a mérlegen

Mikor a homok elkezd hullani, egy darabig csökken a mérleg által mutatott súly. Ennek az oka az, hogy a levegőben levő homok szabadon esik, így nem terheli az alátámasztást. Ha a homok egyenletes dm/dt sebességgel pereg át a lyukon, akkor az oszlop tömege, mikor a homok eléri az óra alját:
m=dm/dt*t, ahol t az idő, amíg a homok leér az óra aljára. Ha ehhez l hosszon kell esni a homoknak, akkor a szabadesés miatt
l=g/2*t² és így
m=dm/dt*sqrt(2*l/g). A homok v=gt sebességgel csapódik be, így dt idő alatt a becsapódó homok gyorsulása (lassulása)
a=g*sqrt(2*l/g)/dt. Így a homok lefékezéséhez
F=m*a=dm*g*sqrt(2*l/g)/dt erőre van szükség. Vegyük észre, hogy ez éppen megegyezik a levegőben levő homokoszlop súlyával. Így tehát, onnantól, hogy az első homokszem leér, a mérleg visszaugrik az eredeti állásba, és pont annyit mutat, mintha nem is peregne a homok.
A folyamat végén a jelenség fordítva játszódik le: az erő elkezd nőni, ahogy csökken a levegőben levő homokoszlop hossza, és egészen addig nő, amíg az utolsó homokszem le nem ért. Ekkor megint visszaugrik a homokoszlop súlyának megfelelő állásba a mérleg.

A két golyó

A két golyó tömegközéppontja eltérő irányban mozdul el, mikor a golyók a melegítés hatására kitágulnak. Az asztalon levő golyó tömegközéppontja megemelkedik, a fellógatott golyóé lejjebb megy. Ezáltal a két golyó helyzeti energiája nem egyformán változik. A fellógatott golyó helyzeti energiája csökken, a másiké nő, és ebből az energiakülönbségből adódóan jobban felmelegszik a felakasztott golyó. (Ne akard kimérni. ;-)))

Ide-oda forgó ventillátor

A ventillátor forgását a fénycső világítja meg. Az izzólámpával ellentétben a fénycső másodpercenként százszor (a hálózati 50 Hz-es feszültség minden félhullámában) kigyullad, majd elalszik. Az emberi szem lassúsága miatt az így látott állóképek sorát folyamatosnak érzékeljük. Akkor látjuk úgy először, hogy a ventillátor forgásirányt vált, mikor a gyorsuló forgás miatt két felvillanás között 1/6-nál többet fordul. Az agynak ugyanis ilyenkor "kézenfekvőbb" azt feltételezni, hogy a ventillátor visszafelé fordult kevesebbet, mint hogy előrefelé sokat. A második irányváltást akkor érzékeljük, mikor 3/6-ot fordul a kerék két felvillanás között. És végül a harmadikat akkor, mikor 5/6-ot. Ezek után, tovább növelve a fodulatszámot, a ventillátort megállni látjuk, vagyis a két felvillanáskor pont ugyanúgy áll a kerék (elvileg elég lenne az, hogy 120 fok többszörösét fordulja a kerék, de a jelen speciális esetben pont egy egészet fog fordulni, mert az 5/6 fordulatnál nagyobb létező, 120 fokkal osztható legkisebb elfordulás a 6/6, vagyis az egy egész. Így a ventillátor fordulatszáma pontosan 100 fordulat/perc ilyenkor.

Féktárcsa (autósoknak)

Legyen az autó tömege 1200 kg, sebessége 100 km/h. Egy rendes autó ekkora sebességről 3 másodperc alatt megáll, ezalatt a mozgási energia hővé (súrlódási munkává) alakul a fékeken. A mozgási energia
m/2*v²=600*(100/3.6)²=463 kJ. Ez tűnik el 3 másodperc alatt 4 tárcsán, vagyis féktárcsánként közel 39 kW (!!! A családi házunkat egy darab 35 kW-os kazán fűti!) a fűtőteljesítmény.

Tolóerő (autósoknak)

Az autó tömege legyen megint 1200 kg, gyorsulás 0-ról 100 km/h-ra 8 másodperc (nem egy világbajnok érték, de a feladathoz teljesen jó). Ekkor, egyenletes gyorsulást feltételezve
F=m*a, és tudjuk hogy
a*8=27.8 m/s, vagyis a=3.47 m/s², és így
F=1200*3.47 N=4166 N. Ha két kerék tolja az autót, akkor ez kerekenként kb. 2000 N, ami ugye négy zsák cement súlya. Ez az az erő, amit a gumi közvetít az aszfaltra. Ugye már sejthető, miért nem vagyok híve a futózott guminak...
Ezek után saccold meg, mit csinál a 911-es Porsche egyesben, mikor mondjuk 1 másodperc alatt éri el a 40-45 km/h-t... :-/

Hűtőszekrény

Nyitáskor szobahőmérsékletű levegő áramlik a hűtőbe, ami az ajtó becsukása után gyorsan lehűl.
A nyitott hűtőbe áramló szobahőmérsékletű levegő (kb. 300 K) gyorsan lehűl (kb. 260 K-re). A térfogat állandónak tekinthető, így a nyomáscsökkenés kb. 0.13*10⁵ Pa. Ha a hűtő ajtaja mondjuk 40*60 cm, akkor az ebből adódó erő:
F=p*A=0.13*10⁵ Pa*0.24 m² = 312 N.
Mivel egy egyenletesen eloszlik a felületen, az erőkar feleakkora, mint az az erőkar, amin mi az ajtót próbáljuk kinyitni (mivel a forgástengelyhez képest a kilincs az átellenes oldalon van. Így 156 N erő kell.
Mivel a hűtőgép ajtaja nem zár tökéletesen, ezért hosszú idő alatt kiegyenlítődik a nyomás. Emiatt könnyű az első esetben kinyitni az ajtót.

Kátyú

Első becslés: mit is tekintsünk a kerékre mért "elég nagy" ütésnek? Már sportosnak tekinthető és relatív gyakori gumiméret mondjuk a 195/50R15. Ennél a gumi oldalfala kb. 10 cm, így első közelítésben mondjuk azt, hogy az 5 cm-nél nagyobb felütések, amik már a felére nyomják a gumit, durvának tekintendők.
A 15"-os felni sugara kb. 19 cm, így a teljes keréké 29 cm. Ebből kiszámíthatjuk (Pitagorasz tétellel), mekkora a legkisebb olyan gödör, amibe a kerék egyáltalán bele tud süllyedni 5 cm-t. Az eredmény elég nagy: 32 cm. Ráadásul ehhez olyan lassan kell menni, hogy a kerék még csak félúton legyen a gödör fölött, és már meglegyen az 5 cm kitérés.
Az autó egy kereke, pontosabban a lengéscsillapított tömeg kb. 30 kg. Az autó maga kerekek nélkül kb. 1200 kg. Ha minden kerékre egyenlő súly jut, akkor kerekenként 300 kg-nak megfelelő erő feszíti a rugót. Így abban a pillanatban, amikor a kerék a gödör fölé ér és eltűnik alóla a talaj (ez nyilván nem pillanatszerű, de elfogadható közelítés, mivel a kerék lefelé elmozdulása az idő négyzetével arányos), a gravitáció és a rugóerő együttesen 11 g-vel fogja lefelé tolni a kereket. Ez bizony nem kis érték...
Tegyük fel, hogy a rugóerő kitéréstől függetlenül állandó. Ez nyilván nem igaz, de a rugóút első pár cm-én elfogadható (felső!) becslés, főleg gyári rugóknál, ahol a rugóút meghaladja a 10 cm-t.
Ha a gödör szélessége x (m), akkor a megtételéhez szükséges idő:
x=v*t alapján
t=x/v=x/20 (m/s).
Az állandó erővel gyorsított kerék elmozdulása mindeközben:
y=a/2*t²=5.5*10*x²/400 (m)=0.1375*x² (m).
Ez mondjuk a fent kiszámított 32 cm széles gödör esetében 1,4 cm... lenne, de eddigre már átértünk a gödör fölött. Ezt alig fogjuk megérezni.
A kérdés tehát az, hogy mekkora lesz az a gödör, aminél 5 cm-re bemegy a kerék és éppen ebben a pillanatban koppan fel a kátyú túlsó peremén. Az 5 cm elmozdulás kb. 60 cm-es útnál következik be ennél a sebességnél, ehhez hozzá jön a kerék középpontjának függőleges vetülete és az ütközési pont közötti 16 cm, tehát összességében 76 cm széles gödör lesz a határ. Ez azért már nem kis kátyú.
Vegyük észre, hogy az eredmény a gödör szélessége mellett a sebességtől is négyzetesen függ. Tehát 36 km/óránál már a 15 + 16 = 31 cm átmérőjű gödör (ami jó közelítéssel 32 ;-)), is akkora felütést okoz, mint 72 km/óránál a 76 cm.
Tehát ha kátyút látunk, és már nincs időnk kikerülni: padlógáz! :-)

Barátom, Norbi kommentjei alapján néhány kiegészítés:
A kerékátmérőtől is erősen függ a sebességfüggés tartománya, nagy terepjáró esetén (majdnem 80 cm-es kerékátmérő) egy 15 centis gödröt semmilyen sebességgel nem fogunk megérezni, mert a kerék súlypontja számottevően nem ereszkedik, hiszen a gumi hamar felfekszik a gödör peremén. Továbbá a sebességtől a "durva felkoppanás" nemcsak a függőleges, hanem a vízszintes mozgáskomponens miatt is függ, csak ott a sebességgel nem fordított, hanem egyenes arányban. Azaz ha pl. öt km/órával belemegyünk egy 50 cm átmérőjű gödörbe, korántsem fog olyan "durván felkoppanni" a kerék, mint mondjuk 40-nél. Azaz igaz, hogy átrepülni nagyobb sebességgel könnyebb a gödör fölött, de ha sehogy sem megy az átrepülés, akkor viszont minél lassabban mész, annál kisebb lesz az elkerülhetetlen koppanás. Tehát nem olyan egyszerű a tanács, hogy "padlógáz", hanem a gödör méretétől és távolságától, az autó sebességétől és lassulási illetve gyorsulási képességeitől függően kell egy bonyolult döntést hozni arról, hogy érdemes-e megpróbálni az adott helyzetben átrepülni, vagy inkább lassítsunk amennyire lehet, hogy az elkerülhetetlen huppanás minél kisebb legyen. És akkor még bele sem kevertük azt, hogy ha az autó nem egyenletes sebességgel, hanem lassulva vagy gyorsulva megy bele a gödörbe, akkor nem egyforma az első és a hátsó kerekeken ébredő függőleges erő, ami a kereket a kátyúba löki. Ez is változtat a döntési paramétereken, mert ha padlófékkel csúszunk a gödörbe, nagyobb a koppanás, mintha csak úgy belegurulunk.

Acélkötél

Reális becslés, hogy 1 mm² keresztmetszetű acélkötél terhelhetősége valahol 60 és 600 kg között lehet. Azért pont ezekkel a számokkal becslünk, mert a Föld tömege 6 * 10²⁴ kg. Így a felfüggesztéshez valahol 10²² és 10²³ mm² közötti keresztmetszetű acélkötél kell. Ez pedig alsó becslésben 10²² = R² * Pi, ahonnan
R = 32 * 10¹⁰ mm = 32 * 10⁷ m = 32 * 10⁴ km = 320,000 km.
Ez pedig alig kevesebb, mint a Hold-Föld távolság. És ez még csak a kötél sugara...

A majmok esete a Hamlet szövegkönyvvel

A Hamlet eredetiben kb. 30 ezer szóból áll, egy szó átlagosan 5 betű, ez 150 ezer karakter. Tegyük fel, hogy ebben benne vannak a szóközök és az írásjelek. Az angol abc-ben 26 betű van, mindegyikből lehet kis és nagybetű. Ehhez vegyünk hozzá 10 féle számjegyet, és 6 írásjelet (a 4. az angolban gyakori aposztróf, az 5. a vessző, a 6. a szóköz). Nagyságrendileg 2⁶ különféle karaktert kapunk. Ha ebből a betűkészletből akarunk kirakni 150,000 karakter hosszú szöveget, (2⁶)^150,000 féle szöveget tudunk alkotni. Figyelembe véve, hogy 2¹⁰ az kb. 10³, a lehetséges szövegváltozatok száma kb. 10^270,000.
Ha majmaink mondjuk 5 leütés/másodperc tempóban gépelnek, akkor egy verzió legépelése 150,000/5 másodperc, vagyis kb. 41,7 óra. Évente egy majom 365 * 24 / 41,7 = 210,24 Hamletet gépel le. Ha a világegyetem életkorát 15 milliárd évnek vesszük (ennél kevesebb, de belefér), akkor egy majom az ősrobbanás óta 3,15*10¹² Hamlet változatot gépelt le.
Egy galaxis 10⁷-10¹⁴ számú csillagot tartalmaz. A világegyetem ismert része 10¹²-nél kevesebb galaxist tartalmaz. Így csillagonként egy bolygóval számolva nagyságrendileg 10²² bolygót becsülhetünk.
A Föld nagyjából 6*10²⁴ kg. Ha hidrogénből lenne, amelynek a móltömege 2g (molekula!), akkor 3,6*10⁵¹ atomból állna. Mivel a legtöbb elem nehezebb (sokkal), becsülhetjük az atomok számát 3,6*10⁵⁰-nel.
Ha a Föld minden atomjára egy majom jutna, akkor a világegyetemben mostanáig 3,15*10¹² * 10²² * 3,6*10⁵⁰, azaz kb. 10⁸⁵ különböző Hamlet készül el. Ez áll szemben a 10^270,000 különböző lehetséges Hamlet változattal. Vagyis a Föld egy atomjára egynél több majom jut (elképzelhetetlenül sokszor több).

Kerítésfestés hármasban

Tegyük fel, hogy a ténylegesen lefestendő kerítés mellett van egy másik kerítés, aminek a festésével ugyanolyan tempóban lehet haladni.
Nevezzük a három testvért A, B, C-nek.
Amíg A fest, addig B és C fesse a másik kerítést. Amikor A abbahagyta, a második kerítésen egy fél kerítésnyi szakasz van lefestve. Ezután amíg B fest, A és C fesse a másik kerítést. Amikor B abbahagyta, a másik kerítésen már kétszer fél kerítésnyi szakasz van lefestve. Hasonlóképpen, mire C lefesti a maga részét, addigra (1) kész a lefestendő kerítés, és (2) a második kerítésen másfél kerítésnyi szakasz van lefestve. A, B és C együtt így 2,5 kerítésnyit festettek. Ezért, ha egyszerre festik ugyanazt a kerítést, akkor két és félszer gyorsabban készülnek el (az eredetileg szükséges időnek csak a 40%-a szükséges a munka elvégzéséhez).

Gyümölcsösládák

Kiveszünk a "vegyes" feliratú ládából egy gyümölcsöt. Mivel a "vegyes" felirat nem stimmel, csak olyan gyümölcs van benne, amit kivettem. Az a láda, amelyiken a másik gyümölcs neve van, a vegyes láda, és az a láda, amelyiken a vegyes felirat van, abban van a másik gyümölcs.
Tehát egy húzás elegendő.

2012 a 2012-en

1. lépés: B alsó és felső korlátjának meghatározása
Mivel
2012 < 10^4,
2012^2012 < 10^(4*2012) = 10^8048, tehát
2012^2012 legfeljebb 8049 jegyű (ennél jóval kevesebb jegyű, de elég ez a közelítés).
Emiatt 2012^2012 jegyeinek összege < 8049 * 9 (mert az utolsó jegy biztosan nem 9), azaz A < 72441.
B akkor érheti el a maximumát, amikor A = 69999, ez könnyen belátható.
Ekkor B értéke 42.
B jegyeinek összege akkor érheti el a maximumát, amikor B = 39, szintén könnyen belátható. B jegyeinek összege ekkor 12.
Így B jegyeinek összege 1 és 12 között kell, hogy legyen.
2. lépés: B 9-cel való osztási maradéka
2012 = 4 * 503 = 4 * (9*56 – 1) és 2^3 = 8 = (9-1). Ezeket felhasználva:
2012^2012 = 4^2012 * 503^2012 = 2^4096 * 503^2012 = 2 * 8^1365 * 503^2012 = 2 * {(9-1)^1365} * {(9*56-1)^2012}
A kapcsos zárójelekben levő szorzatok kifejtésekor az összes részletszorzat osztható lesz 9-cel, kivéve az utolsót, ami az elsőnél -1, a másodiknál +1 (a páratlan, illetve páros kitevő miatt). Így a teljes kifejezés felírható 9*K – 2 alakban, vagyis a 9-es osztási maradéka 7.
Mivel a 9-cel való oszthatóság szabálya az, hogy ha a szám osztható 9-cel, akkor a jegyeinek összege is osztható 9-cel, ugyanez igaz a szám és jegyeinek összege 9-es osztási maradékára is. Ezért A 9-es osztási maradéka is 7, és hasonlóképpen, B 9-es osztási maradéka szintén 7.
3. lépés: Konklúzió
Mivel az 1 és 12 tartományban csak a 7-re igaz, hogy a 9-es osztási maradéka 7, ezért B = 7, és így a számjegyeinek összege 7.

A horgász pipája

Amikor a pipa horgász szájában van, a csónak mélyebben van, mint ha nincs benne, méghozzá a pipa súlyának megfelelő vízmennyiséggel szorít ki többet. Amikor a horgász kiejti a pipát, a csónak ennyivel feljebb jön, vagyis a vízszint lemegy (dh1). A vízbe esett pipa vizet szorít ki, ettől a vízszint megemelkedik (dh2). A feladat szerint:
abs (dh1 + dh2) = dh2.
Három esetet érdemes megkülönböztetni:
1. A pipa sűrűsége egyenlő a levegőével. Ez esetben nincs vízszintváltozás, dh1 = 0, dh2 = 0, tehát ez matematikailag jó megoldás, de sajnos a való életben nem nagyon találunk ilyen pipát. :-)
2. A pipa sűrűsége kisebb a vízénél. Ez esetben a pipa úszik a vízen. A vízbe esett pipa a saját súlyának megfelelő vizet szorít ki függetlenül attól, hogy honnan esett a vízbe, és amíg a csónakban volt, addig is ennyi vizet szorított ki, vagyis dh1 + dh2 = 0, vagyis dh2 = 0, ez az első esetre vezet vissza.
3. A pipa sűrűsége nagyobb a vízénél. Ilyenkor a pipa a vízbe esve elmerül, vagyis a saját térfogatának megfelelő vizet szorít ki, míg a csónakban a saját súlyának megfelelő vizet. Ilyenkor az egyenlet úgyis megoldható, ha dh1 + dh2 < 0, ekkor
- dh1 - dh2 = dh2
-dh1 = 2 * dh2
Vagyis a pipa súlyának megfelelő víz kétszer annyi, mint a pipa térfogatának megfelelő víz, tehát a pipa sűrűsége kétszerese a vízének.

n*n-es sakktábla bejárása

Legyen a felfelé lépések száma X. Akkor a balra lefelé lépések száma is X, mivel ugyanabba a sorba érkezünk, ahonnan indultunk. A jobbra lépések száma viszont X+1, mivel eggyel jobbra érkeztünk a kezdeti pozícióhoz képest.
Összesen 3X+1 lépés volt, és ezzel N²-1 lépést tettünk meg, hiszen a tábla N*N-es.
Vagyis 3X+2 = N².
A négyzetszámok viszont sosem 3X+2 alakúak, tehát a bejárás nem kivitelezhető.

Farkas, kecske, ... oroszlán

Wolkens megoldása
Jelöljük az állatok táplálkozásának számát a következőképpen:
OF: oroszlán eszik farkast
OK: oroszlán eszik kecskét
FK: farkas eszik kecskét
Az állatok számának változásai:
(1) Oroszlánok: 6 - OF - OK + FK
(2) Kecskék: 17 + OF - OK - FK
(3) Farkasok: 55 - OF + OK - FK
A három számból kettőnek nullának kell lenni a végén.
(1) + (2)-t összeadva (csak farkas marad):
23 - 2 * OK = 0 -> OK nem egész szám, nem lehetséges.
(1) + (3)-t összeadva (csak kecske marad):
61 - 2 * OF = 0 -> OF nem egész szám, nem lehetséges.
(2) + (3)-t összeadva (csak oroszlán marad):
72 - 2 * FK = 0 -> FK = 36
Ebből:
17 + OF - OK - 36 = 0
55 - OF + OK - 36 = 0
Kivonva:
38 - 2 * (OF - OK) = 0
OF - OK = 19
A legkevesebb állat akkor fogy, ha OK = 0, OF = 19. Ekkor 78 - 36 - 19 = 23 állat marad.
Ez kivitelezhető, egy lehetséges sorrend:
- 17 farkas megeszik 17 kecskét: marad 23 oroszlán, 38 farkas, 0 kecske
- 19 oroszlán megeszik 19 farkast: marad 4 oroszlán, 19 farkas, 19 kecske
- 19 farkas megeszik 19 kecskét: marad 23 oroszlán, 0 farkas, 0 kecske

Norbi megoldása
1. A nyugalmi állapot nyilván az, ha csak egyféle állat marad.
2. Látni kell, hogy mindhárom tranzakció bármely két állat vonatkozásában azok összesített számosságát vagy 0-val, vagy -2-vel változtatja meg. Azaz amelyik állatpár paritása nem egyforma, az a kettő nem tud egyszerre elfogyni, azaz a harmadik állat nem lehet a megmaradó faj.
3. A kiinduló számok miatt csak az oroszlán lehet a megmaradó faj.
4. Oroszlánt úgy lehet szaporítani, ha egy kecske és egy farkas eltűnik. Tehát a 17 kecskét megeszi 17 farkas. Így lesz 23 oroszlán és 38 farkas.
5. A 38 farkas kétlépéses körökben kettesével eltünteti magát úgy, hogy az oroszlánok száma nem változik: OF-K, FK-O.

Szilvi megoldása
Csak akkor fogynak el, ha pont annyi kecske van, mint amennyi valamelyik ragadozó. Mivel minden kajálás után kevesebb állat van, és kecske csak úgy "jöhet létre", ha oroszlán farkast eszik, illetve oroszlán csak kecske + farkas kombóból, ezért az oroszlán + kecske száma maximalizálja a létszámot. A maximális kecskeszámot kell meghatározni, az pedig adódik a 17 + 6 kecske + oroszlán számából = 23.
Itt már csak addig kell zabbantani, míg előáll a 23 kecske és 23 farkas -> 23 oroszlán.

Gabi megoldása
1. A különbségek paritása miatt oroszlánok maradnak a végén.
2. Ekkor el kell fogyasztani az összes farkast, ez minimum 55 fogyás, annyival meg is oldható, tehát 17 + 6 = 23 oroszlán marad.

A hangya meg a pálca

1.) Mivel a hangya víszintesen indul el a pálcán v sebességgel, a pálca ugyanazon vége pedig v sebességgel kezd emelkedni, az eredő sebesség iránya 45 fok lesz a vízszinteshez képest.

Jelöljük h-val egy adott pillanatban a pálca emelkedő végének magasságát. A hangya ekkor már h hossznyit végigment a pálcán. Jelöljük továbbá xp-vel a pálca asztalon levő végének az emelkedő végpont függőleges vetületétől való távolságát, x-szel a hangyának az emelkedő végpont függőleges vetületétől való távolságát, y-nal pedig a hangya magasságát.

2.) Pithagorasz tétele alapján
xp² + h² = 20² Hasonlóságot felismerve - felírhatjuk, hogy
x/xp = h/20 Innen
xp = 20*x/h Behelyettesítve az előzőbe
(20*x/h)² = 20² - x² Rendezve 20²*x² = h² * (20² - h²) Jelöljük h²-et a-val, ekkor az egyenlet 20²*x² = a * (20² - a) alakot kap. Kifejtve a² - 400*a + 20²*x² = 0 Teljes négyzetté alakítva
(a-200)² - 40000 + 400*x² = 0 Ebben x akkor lesz maximális, amikor a-200 = 0, és ekkor x = 10, vagyis a hangya a legtávolabbi ponton 10 cm-re van vízszintesen.

3.) Hasonlóságot felismerve - felírhatjuk, hogy
h/20 = (h-y)/h Ezt rendezve
h² -20*h + 20*y = 0 Teljes négyzetté alakítva
(h-10)² - 100 + 20*y = 0 Ebben y akkor lesz maximális, amikor h-10 = 0, és ekkor y = 5, vagyis a hangya a legmagasabb ponton 5 cm-en van.

A banán hossza

Vezessük be a következő jelöléseket:
- a kötél hossza "l" láb
- a majom súlya "mm"
- a banán súlya "mb"
- a súly súlya "ms"
- a majom kora "km"
- a majom anyja kora "ka"
A kötél fajlagos súlya 1/3 font/láb. A banán fajlagos súlya 2 uncia/hüvelyk.
Felírhatjuk, hogy
ms = mm + mb (1)
l(láb) = km(év) (2)
mm(uncia) = ka (3)
km + ka = 30(év) (4)
mm / 2 + mb = (mk + ms) / 4 (5)
A majom anyja feleannyi idős (T0), mint amennyi a majom lesz akkor (T1), amikor háromszor annyi idős lesz, mint az anyja volt akkor (T2), amikor feleannyi idős volt, mint a majom lesz akkor (T3), amikor annyi idős lesz, mint amennyi az anyja lesz akkor (T4), amikor négyszer annyi idős lesz, mint a majom volt akkor (T5), amikor kétszer annyi idős volt, mint az anyja volt akkor (T6), amikor harmadannyi idős volt, mint a majom volt akkor (T7), amikor annyi idős volt, mint az anyja volt akkor (T8), amikor háromszor annyi idős volt, mint a majom volt akkor (T9), amikor negyedannyi idős volt, mint most.
T9-ben a majom km/4 éves, tehát T8-ban a mama 3/4*km éves.
T7-ben a majom 3/4*km éves.
T6-ban a mama 1/4*km éves.
T5-ben a majom 2*1/4*km = 1/2*km éves.
T4-ben a mama 4*1/2*km = 2*km éves lesz.
T3-ban a majom 2*km éves lesz.
T2-ben a mama 1/2*2*km = km éves volt.
T1-ben a majom 3*km éves lesz.
T0-ban a mama 3/2*km éves.
(4)-ből km + 3/2*km = 30
5/2*km = 30
km = 12
ka = 18
(3)-ból a majom súlya 18 uncia.
(2)-ből a kötél hossza 12 láb.
A kötél súlya 1/3 font/láb * 12 láb = 4 font = 64 uncia.
(1)-ből beírva ms-t (5)-be:
mm/2 + mb = (mk + mm + mb) / 4. Unciában beírva a számokat:
18/2 + mb = (64 + 18 + mb) / 4
4 * (9 + mb) = 64 + 18 + mb
36 + 4 * mb = 82 + mb
3 * mb = 46
mb = 15 1/3 uncia
A banán hossza 15 1/3 uncia / 2 uncia/hüvelyk = 23/3 hüvelyk = 7 2/3 hüvelyk.

Egy számjegy áthelyezése

A megoldás:
101 - 10² = 1

A téglalap meg a körök

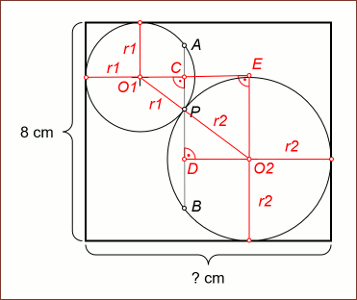Jelöljük a körök középpontját O1-gyel és O2-vel. A sugaruk legyen r1 és r2. Húzzunk merőlegest O1-ből és O2-ből az AB szakaszra, a metszéspontok legyenek C és D. Jelöljük meg a körök és a téglalap érintési pontjait. AC felezi az AP szakaszt, PD felezi a PB szakaszt, így CD hossza 3 cm. Hosszabbítsuk meg az O1C szakaszt és bocsássunk rá merőlegest O2-ből, a metszéspont legyen E ( Nem esik a kör kerületére! ). CDO2E téglalap, mivel minden szöge derékszög, így CD = O2E. Az ábrából láthatóan r1 + O2E + r2 = 8 cm, azaz r1 + r2 = 5 cm. Az O1EO2 derékszögű háromszögre felírva a Pithagorasz tételt: 3^2 + O1E^2 = (r1 + r2)^2 O1E^2 = 25 – 9 = 16, azaz OE1 = 4 (cm). Az ábrából láthatóan a téglalap hosszabb oldala r1 + O1E + r2, azaz 5 + 4 = 9 (cm).

A cikk utoljára frissítve: 2023.01.

Vissza a lap tetejére | Vissza a nyitóoldalra